by Den Blonde Ulven
July 19, 2023
My father and I performed some optic experiments near Virginia Beach in Norfolk, Virginia. The goal of this event was to check the hypothesis: can objects be seen further than they should be able due to the curvature of the Earth?
We were standing on Ocean View Beach close to East Ocean View Beach- coordinates 36.933410, -76.201875. Three pieces of equipment were utilized- a Nikon P1000 camera, a tripod, and an SD memory card for the camera. This camera was capable of recording while shooting a video and simultaneously zooming in great distances. The P1000 is what captured the videos shown.
The weather was partly cloudy, no rain, and slightly hazy. These are not ideal conditions due to the haze. Yet even under these non-ideal conditions, objects that have been zoomed in upon are distinguishable.
We used a website to determine the location of cargo ships on a map in near real-time: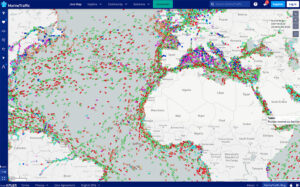
This allowed us to estimate where the ships were. We then used a feature on Google Maps called “measure” to connect our location with the ships’. This gave us an approximate distance of which I estimate is accurate within a range of (+-)0.2 miles.
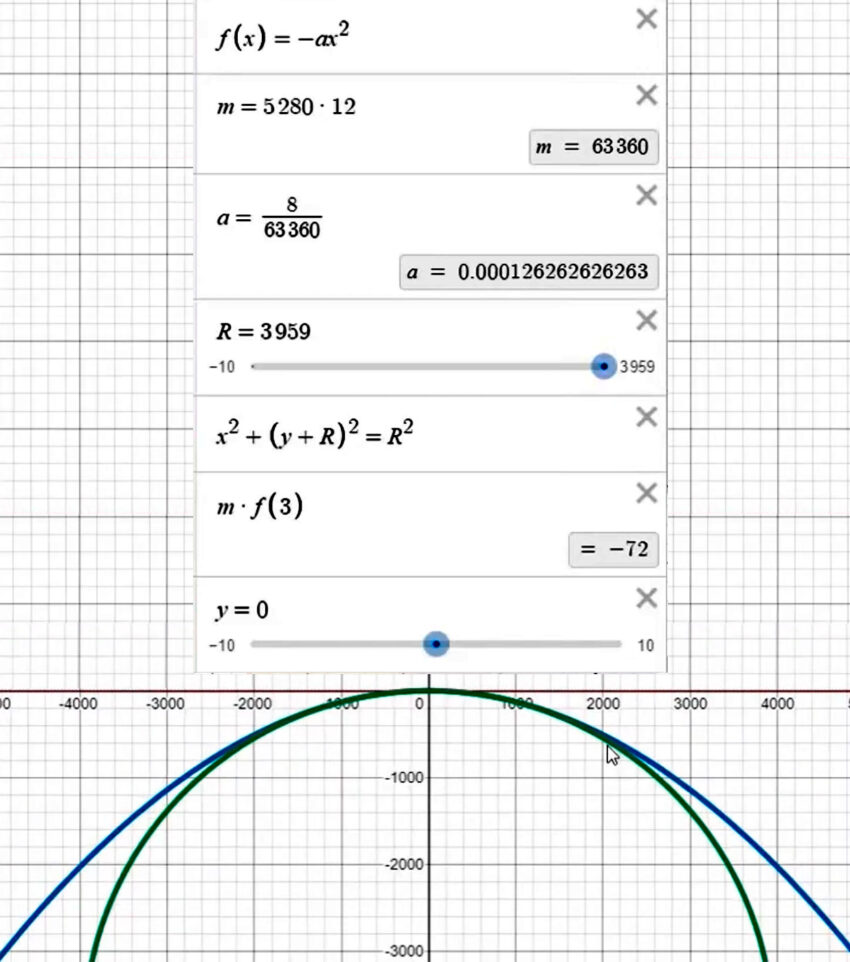
We used the equation of 8 inches per mile squared (y = 8 * x^2) as a very-close approximation to calculate the curvature of the earth, where x is the distance away from a viewed object in miles, and y is the amount of height lost in inches. This equation makes a parabola, whereas the more exact equation to use is circular. The parabolic equation diverges from the circular equation at thousands of miles away. For this experiment, we were concerned with possible miles, not even tens of miles. This difference is so negligible as to serve this experiment’s purposes.
To give a few examples, at 1 mile away, 8 inches of height is lost. 2 miles away, 32 inches is lost. 3 miles, 72 inches, etc. This is offset by the point of view of the viewer being x feet above the surface. In all of the shown videos, the camera is 6 feet above the water. When factoring in this offset, simply subtract 6 feet after calculating the amount of height lost.
The full equation is
y = [(8 * x^2) / 12] – 6
where x is the amount of miles away from the viewed object
To use some video examples, the most significant are those at a distance of 6+ miles. The bridge in the following video is 6.4 miles away; the boat 6.5:
https://www.bitchute.com/video/HHQLpBqbdNfp/
Taking the above boat with the boat being 6.5 miles away. The math looks like this:
[(8 * 6.5^2) / 12] – 6 = 22.16 feet
So, at a distance of 6.5 miles away, we should lose about 22 feet of height. In the above example, we can see the entire side of the ship all the way down to the water line. In other video examples, the boat is clearer:
https://www.bitchute.com/video/cIvu7IPcmsCN/
Where the water meets the boat is clear, and the entire shape is clearly shown. In the 6.5 miles example, the entire shape is still visible. The water meeting the boat might not be clear, but the lack of lost shape shows how little of the boat has been lost to the horizon. Typical cargo ships in the US do not exceed 116 feet in height above the water level. Thus, we should lose 1/5 of the boat’s bottom, and yet we see much more.
We also captured video with a pier as an object. The end of the pier is 3.6 miles away from our position:
https://www.bitchute.com/video/N4wFljePouq6/
Taking the above pier example, the pier is 3.6 miles away. The math looks like this:
[(8 * 3.6^2) / 12] – 6 = 2.64 feet
So, at a distance of 3.6 miles away, we should lose 2.64 feet of height. The footage is clear- we can see where the water meets the supports of the pier.
There are a few videos in which the distance to the viewed objects are unknown. We were unable to identify exactly what was viewed and matching it to a map. The haze also significantly affects the viewing quality of these objects. What is known is that they are well beyond 6.5 miles away. One is a bridge with many pillar supports:
https://www.bitchute.com/video/xHzytl0mhPAE/
https://www.bitchute.com/video/kAf72fyQ9mmy/
The other appears to be a white building, possibly next to the water:
https://www.bitchute.com/video/dqlVPv3ac3N3/
Because these objects are of unknown distances, no exact calculation can be made. If anyone can identify what/where this building or bridge are, please share them or the coordinates with me.
There is another phenomenon of which has hitherto been unaccounted. That is the phenomenon of refraction, or the bending of light. The argument is that the medium light travels though bends it, so any object that we view is actually slightly distorted and is being warped around the curvature. This adds back some amount of lost height an object experiences as it moves away from a point due to the curvature. I have read many different accounts giving a range of values as to how much height is added back due to refraction. It apparently deals with the position of the sun, particles in the air, and other factors. I am unsure how to account for this in my equations. If this is known by someone, please share.
Several additional videos were captured, but either the positioning was not ideal, the distance too small to be significant, or other factors prevented them from being stellar examples. These have been included here for completeness:
https://www.bitchute.com/video/g2VAenZ71Lnb/
https://www.bitchute.com/video/rAF7m7Jxw5GN/
https://www.bitchute.com/video/ZE4lnuPRGONp/
https://www.bitchute.com/video/G7QSOoZSU76I/
https://www.bitchute.com/video/T5uDMS65f8QV/
https://www.bitchute.com/video/O8DQ8ip4Kjny/
https://www.bitchute.com/video/nw3AJ7Y3BBdO/
In conclusion, I have seen with my own eyes, via technology generally available, further than I should be able to see. This confirms to me that the Earth is not a ball with a radius of 3,963 miles. It could be a ball of significantly larger radius, or a flat plane, or a turtle with a calendar on the back of its shell. What it is absolutely not is a ball the size NASA and Science Religionists claim it to be. However, based on our work and the work of others performing different experiments, pilot testimonies, and other factors, I do not believe it a ball at all.
Notes:
I am not a photographer.
It is very difficult to precisely and smoothly record clearly while zoomed in such extreme distances.
The 8 inches per mile squared came from various Earth skeptics. But this video does a good job visualizing the math and showing that the approximation eventually breaks.
MathAdam — approximating the curvature of the globe
Regarding refraction- I do not necessarily believe the mainstream view of this phenomenon. It seems like rationalization to account for people being able to see further than they normally should. Even still, I think that at far enough distances, the amount we are able to see absolutely dwarfs the maximum amount of height added back by refraction.
____________
You can find me on Social Galactic. I attempt to post at least once a day @DenBlondeUlven.
You can also email me – denblondeulven@protonmail.com
On refraction… Air slows light down very slightly compared to a vacuum. Hot air has a slightly lower density. than cold air. The result is light travels just a bit faster in hot air than in cold air.
On a day when the sun shines down on an asphalt highway, the asphalt may become much hotter than the air temperature, so you get a decreasing thermal gradient with respect to height: it’s hot near the ground and cooler as you go up higher. Light curves up, so you will see reflected light from the sky appearing as though it comes from near the ground – a mirage.
The ocean maintains a more stable temperature than the air above it. On a hot day, the air is warmer than the water, so you’d have an increasing thermal gradient. Light will curve down and you will be able to see further than the nominal “straight line” distance.
I suggest you pick the coldest convenient day in the winter and see if you can repeat your result.
I believe your calculations are wrong in how you account for your initial height. Based on the horizon distance calculation you site at 8inches per mile squared you have about three miles before you begin to lose any height.
That seems to align with the photo of the pier. The bottom of the pilings are just barely in view at about three miles making that the horizon distance. The same is true for the boat. It’s at twice that distance meaning it will be about 6ft below the horizon line which is believable based on what I see.
I think you’re failing to account for the angle of view afforded by the 6’ height of the viewer. You can’t just subtract 6’ from the expected drop – you must account for the angle you can now view at 6’ above the surface.
There is no foam on the pier columns, so I doubt you can see the water line, which would confirm not flat.
Also, try this math.
https://flatearthbusted.blogspot.com/2016/08/flat-earth-follies-how-to-derive-8-per.html
consider that google maps, gps, etc gives you the distance on the curve, not a line-of-sight distance.
Apologies, here’s the math/equation page. The other is more of a “why 8″ is wrong” page.
https://flatearthinsanity.blogspot.com/2016/07/derivation-for-height-of-distant.html
Please add the math and deltas for refraction. Showing these numbers would settle doubts readers may have regarding your findings. Cheers.
I’ve been a sailor in the US military, and was employed as a lookout from a submarine on many occasions. I do not remember the exact calculations we used for head math, though I suspect they were very similar to yours.
Your equation can be simplified to y = 2/3*x^2-6. Order of operations happily favors it, and 8/12 is 2/3. Other than calculating for feet, your equation is probably the same as what we used, expressed simply as “height difference of inches is eight times the square of the distance in miles, minus observer height”. It becomes less accurate to the point of absurdity at long ranges, but at just a few miles to a few dozen miles it’s fine.
Refraction does unfortunately have an effect, and it is sometimes a great one. It was enough of one to be noticeable by eye in certain weather conditions as a lookout. It’s related to what temperature the atmosphere is at varying heights, and probably also to humidity. I don’t know the weather conditions where you were doing these tests, but in the right (or wrong) conditions refraction can be pretty extreme. Ships have been seen from up to about fifty miles away on the open ocean in certain conditions, which seems nuts until you’ve seen it, considering they should be closer to two thousand feet below the horizon at that point if not for the atmospheric lensing effect.
IIRC there are also certain locations on the Earth that are infamous for refraction by very often having certain weather conditions. There’s a canal or river somewhere that you can supposedly see about 200 miles down the length of at times during the day.
Fata Morganas are a related optical phenomenon where it is a complete and inverted reflection, sometimes at some pretty extreme distances. Seeing someone or something upside down on the sky traveling along is pretty weird.
It is convenient not to believe in mainstream refraction but what is dissident refraction?
Within the right conditions, you can see Corsica from Nice so i’m skeptical about your skepticism.
“Within the right conditions, you can see Corsica from Nice…”
… yes, exactly….
“I can see around the curve for 100+ miles and don’t see a problem with that because Science!”
I do not see a problem with the world being fabulous. Science merely try to explain a phenomenon that everyone can see with their own eyes (it’s a mirage).
We make optical fibers from our understanding of light reflection and refraction. This is pretty great engineering.
That said, modern science is corrupted and I think that seeing science as a religion is at best stupid, at worst diabolical.
About Earth, I trust the Ancient Greeks.
Welcome to the world of globe skepticism. To prepare you for the coming onslaught, you will be called retarded, a moron, told to drink bleach and not to have children, told there are “thousands” of experiments you can do in your backyard to prove a globe, which usually involve looking at the sky, Ive heard it all since 2015 when I myself decided to research the shape of our realm. I don’t know what it is, but I know what it ain’t……….it ain’t what NASA says it is. Good luck, welcome to the club.
ShadoHand – rude and discourteous comments aren’t accepted. Restate your comment without the rancor and I’ll approve it.
That’s a lot of math and effort that was completely wasted. You have to start your calculation of what is below the HORIZON. If the horizon is 20 miles away you can see EVERYTHING up to the 20 miles. At that point, and only at that point, do you start to see the bottoms of ships obscured. (You never mentioned how high your camera was above sea level nor how far the horizon is at that height. Kind of important.)
The ‘8 inches per mile squared’ is an imaginary equation signifying nothing. If you graph that equation you end up with half of a parabola. Who thinks the earth is a parabola? You have to figure out the tangent with the radius. There are hundreds of websites that will do the calculations for you. I’m sure you won’t like the radius part, but you could disprove the calculation if you follow it. But you didn’t. You “proved” your false equation and false understanding of curvature doesn’t work. Ok. Now do a real experiment when you’re ready.
Find out how far the horizon is at your camera height.
Find a ship further away than that.
Use a web calculator to predict how much of the ship should be below the horizon.
Take a picture. I’m sure you’ll find it to be spot on.
Ok gamma
I don’t think you’ve setup the geometry correctly. The drop your calculating isn’t what you’re looking at in the pics and movies. Here’s how to show what I mean. Draw a circle, and then a short line coming off it, representing the viewer height. Now draw a line from the top of the viewer, tangent to the circle at the viewer. It shouldn’t touch the cicle. Now draw another line from the top of the viewer that touches the cicle tangentially and continues on. The first line is what you’re calculating in your post, the second line is what you’re observing.
Well done Mr Ulven. This is the type of work that Newton or Galileo would’ve carried out if they had the technology.
And to add to your observations… In 2010 I was in Orlando for a conference. At around 7:30 PM the speaker said “OK let’s shut down and go outside and watch the shuttle takeoff. “
So the space centre is 60 miles away from Orlando. And since they never taught us the curvature calculation in high school .. though it would benefit surveyors, pilots, mining engineers, artillery officers, submarine pilots, etc I thought “ ok cool we will see this launch “even though the calculation tells us the launch center is somewhere around 2400 feet obscured below the horizon. Don’t forget Florida is flat .. a swamp .. that’s why they have no basements.
What I saw was the bright flash of the ignition. We could be see this 60 miles away. It looked to me like a brazing torch ., almost too bright to look at.
Orlando is slightly higher than the space centre but 60 miles is a long way. The curvature calculator gives a value of 1400 feet that is obscured below the horizon.
Many people watch the shuttle takeoff from Orlando .. it was even on the morning news that morning telling their tv audience they can see it.
But Here’s another funny NASA part .. the shuttle went up about the height of a Florida grapefruit .. held at arms length .. before it went DEAD horizontal.
And I thought “wow that’s weird”. Is it going by road?”
If we could see the space shuttle ignition from Orlando then either the earth is a way bigger ball .. or it’s something else.
But what that is ..I don’t know .. so don’t even ask. I just know what it isn’t.
But for those that believe that it is an 8000 mile ball, like you were taught in grade 1, I have some very happy news .. it’s only 108 more days til Santa Claus!
Thank you for taking the time to perform this experiment. I would like to point out something about the trigonometry which explains the results you got.
Since the camera is 6 feet above the water the falloff is relative to the point about 3 miles from the observer: The line segment tangent to the earth at this point and intersecting with the observer’s eye forms the first leg of a right triangle with the second leg being the radius of the earth and the hypotenuse equal to the radius of the earth plus 6 feet.
Let’s call the angle between the hypotenuse and the second leg ‘A’. We can find the value of this angle using the inverse cosine function. The cosine function is the ratio of the length of the leg adjacent to an angle and the hypotenuse. The inverse cosine function just finds the value of the angle from the its known cosine value:
A = arcos([radius of the earth]/[radius of the earth plus 6 feet])
= arcos(20,903,520 ft / 20,903,526 ft)
= 0.0007576713321 radians
The distance to the horizon is the arclength corresponding to this angle:
arclength / [radius of the earth] = A
arclength = 0.0007576713321 * 20,903,520 ft
= 15,837.99784 ft
= 3 miles
From here you can see that the ship is only 3.5 miles beyond the horizon from the observer.
An arclength of 3.5 miles corresponds to an angle of 0.0008841574125 radians
Using the cosine function again we get:
cos(0.0008841574125) = 20,903,520 / (20,903,520 + x)
x = 20,903,520/(cos(0.0008841574125)) – 20,903,520
= 8.171 feet
The equation you gave is also a fair approximation of the drop.
Using the standard model of the shape of the earth and not accounting for refraction or tides, we would expect only about 8 feet 2 inches of the ship to be obscured.
The pier is at 3.6 miles, so it should basically be entirely visible.
I hope you have found this comment useful.
So how about calculating the “real curvature” that would match the observed results. Then use that rate to predict how much can be seen at a given distance?
You need a relief map of the entire area. What complicates the earth’s surface is how varied it is. The earth is not smooth. It would just be better to use a “flat” plain or desert.